Ben je geïnteresseerd in de wereld van wetenschap & technologie en wil je hier graag meer over lezen? Word dan lid van KIJK!
Is het universum oneindig of komt een ruimtereiziger uiteindelijk weer bij zijn beginpunt uit? Die vraag proberen natuurkundigen te beantwoorden door de oudste straling van het heelal aan een nauwgezet onderzoek te onderwerpen.
Als je met je ruimteschip een willekeurige richting in vliegt, blijf je dan maar nieuwe sterren en sterrenstelsels tegenkomen, hoe ver je ook doorgaat? Of zou het ook zo kunnen zijn dat je op een gegeven moment weer bij je beginpunt uitkomt? Dat het heelal, met andere woorden, niet zo oneindig is als je altijd hoort?
Om die vraag te onderzoeken, kunnen we ons wenden tot de oudste straling van ons heelal. Wat die ons kan vertellen, onderzocht Ralf Aurich, theoretisch natuurkundige aan de Duitse universiteit van Ulm, samen met collega’s.
Lees ook:
Eindig in alle richtingen
Als we het hebben over het heelal op grote schaal, moeten we ons wenden tot de algemene relativiteitstheorie van Albert Einstein. Die vertelt ons hoe de zwaartekracht werkt; hoe planeten, sterren, sterrenstelsels enzovoort elkaar beïnvloeden. Maar hoe het heelal als geheel in elkaar steekt, vertelt deze theorie niet zonder meer.
Een heel belangrijk verschijnsel dat ons kan helpen daar toch achter te komen, is de kosmische achtergrondstraling, die 380.000 jaar na de oerknal ontstond. Eén belangrijk stukje informatie dat deze straling oplevert, is dat het heelal, geometrisch gezien, ‘vlak’ is. Dat wil zeggen: evenwijdige lijnen in ons heelal blíjven ook evenwijdig lopen. Ze neigen op grote afstand niet naar elkaar toe en bewegen niet bij elkaar vandaan, zoals ze zouden doen in een niet-vlak heelal.
Die omschrijving roept misschien het beeld op van een landschap dat zich uitstrekt tot in de verste verte, oftewel: van een oneindig groot heelal. Maar dat hoeft niet per se. Van een plat stuk papier, dat twee dimensies heeft (lengte en breedte), kun je bijvoorbeeld een koker maken. Je rolt dan een van beide dimensies – zeg, de breedte – op. In dat geval is een reis in de lengterichting nog hetzelfde, maar brengt een reis in de breedterichting je terug bij je startpunt. Plak je ook nog eens de uiteinden van je koker aan elkaar, dan krijg je een donut. In dat geval zijn beide dimensies van het stuk papier opgerold. Gevolg: zowel een reis in de lengte- als in de breedterichting brengt je terug bij je startpunt (zie illustratie).
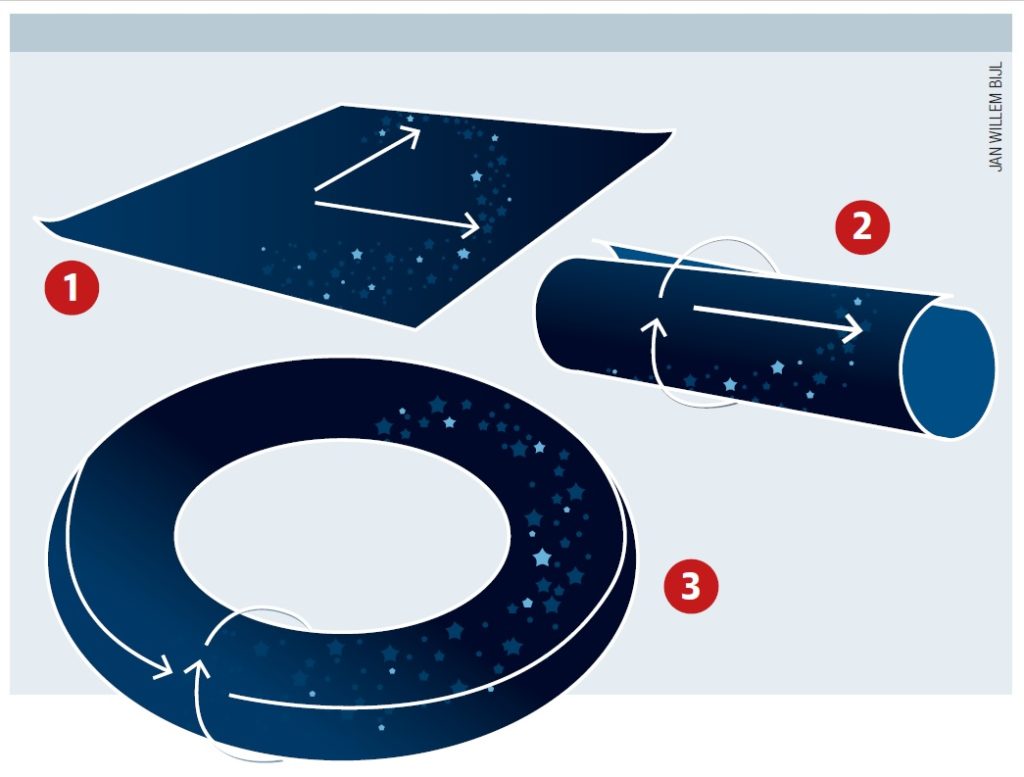
Zo zou ons vlakke heelal ook in elkaar kunnen zitten: een of meer van de ruimtelijke dimensies die het heeft, kunnen opgerold zijn. Geldt dat voor alle drie de dimensies die ons heelal rijk is (lengte, breedte en diepte), dan heeft het geheel de vorm van een zogenoemde 3-torus. En dan is het universum dus eindig in alle richtingen – zonder dat je ooit tegen een muur of iets dergelijks aanloopt.
Veel beter?
En hoe kan de achtergrondstraling ons dan vertellen of dat inderdaad het geval is? Belangrijk om te weten is dat de temperatuur van deze straling niet overal gelijk is; er zitten kleine variaties in. Stel nu dat het heelal in elke richting oneindig is. Dan zouden de temperaturen van twee punten van de achtergrondstraling met elkaar moeten samenhangen, hoe ver die punten ook van elkaar verwijderd zijn. Zijn de dimensies van ons heelal opgerold, dan zou die samenhang moeten verdwijnen als ze zich verder dan een bepaalde afstand van elkaar vandaan bevinden. Het interessante is nu: dat lijkt daadwerkelijk het geval te zijn. En dat kan dus wijzen op een eindig heelal.
Op zich is dat laatste voor ingewijden niets nieuws. Wat Aurich en collega’s aan de discussie toevoegen, is een extra manier om de achtergrondstraling door te lichten op al dan niet opgerolde dimensies. Kort door de bocht kijken ze naar hoe de temperatuur van de straling verandert als je een bepaalde kant op gaat. “Je kunt je voorstellen dat ook die waarde anders is als een of meer van de dimensies zijn opgerold”, zegt kosmoloog Daan Meerburg van de Rijksuniversiteit Groningen, niet betrokken bij de studie.
Op de site LiveScience vertelt Thomas Buchert, een van Aurichs collega’s, wat de uitkomst is van die nieuwe methode: “Een 3-torus sluit veel beter aan op de temperatuurfluctuaties in de achtergrondstraling dan een oneindig heelal.” Dat klinkt haast als een uitgemaakte zaak. Maar Meerburg reageert: “Hoeveel beter is ‘veel beter’? Dat zeggen deze onderzoekers niet in hun artikel.” Wat hem betreft hebben ze vooral laten zien dat hun resultaat in lijn is met wat andere wetenschappers eerder al beschreven.
Drie tot vier keer zo groot
Wel kunnen Aurich, Buchert en collega’s dankzij hun nieuwe methode iets zeggen over de grootte van het heelal – áls het inderdaad zo’n 3-torus is. Ze probeerden in hun computersimulaties namelijk heelallen met allerlei formaten. Daarbij vonden ze het beste resultaat bij een heelal dat drie tot vier keer zo groot is als het waarneembare heelal, het deel van het heelal dat wij vanaf de aarde kunnen bestuderen. Oftewel: ook dit niet-oneindige heelal is nog steeds letterlijk groter dan we kunnen overzien.
Daar komt bij dat het heelal uitdijt; dat sterrenstelsels steeds verder van elkaar vandaan komen te liggen. Gevolg daarvan is dat als je met je ruimteschip het heelal in vliegt, de af te leggen afstand continu groeit. Terugkeren op de plek waar je begon door simpelweg rechtdoor te blijven vliegen, is daardoor stiekem sowieso geen optie, hoe snel of lang je ook reist. En daar veranderen opgerolde dimensies helaas niets aan.
Deze Far Out staat ook in KIJK 2/2022
Bronnen: Classical and Quantum Gravity, arXiv
Beeld: Mehau Kulyk/SPL/ANP